HackTree

 You are given a tree with n nodes. Each node has a value assigned with it. The cost of a path is defined as the summation of all the values assigned to nodes that belong to the path.

The root of the tree is node number 1.

Cost of path example

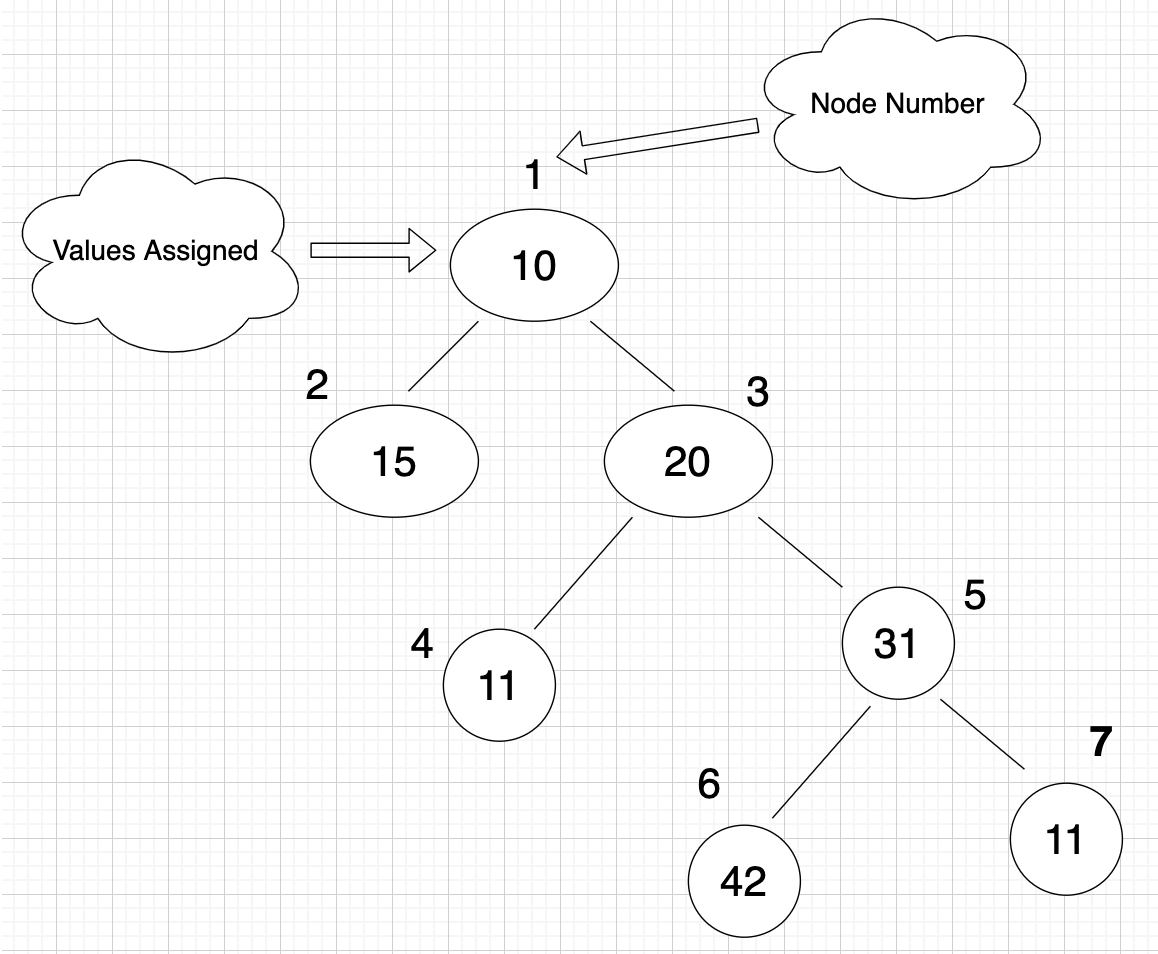
The cost of the path 6 -> 5 -> 3 -> 1 in the above tree is 42 + 31 + 20 + 10 = 103.

A Vertical Path in a tree is the path that is going up towards the root of the tree. It is not necessary for the path to end at the root.

Given a tree with n nodes and an integer k. Find the number of vertical paths such that the (cost of the path) % k = 0 where % represents the modulo operation.

Note: The modulo operation returns the remainder of a division after one number is divided by another. For example - 5 % 2 = 1.

Example

k = 2

tree =

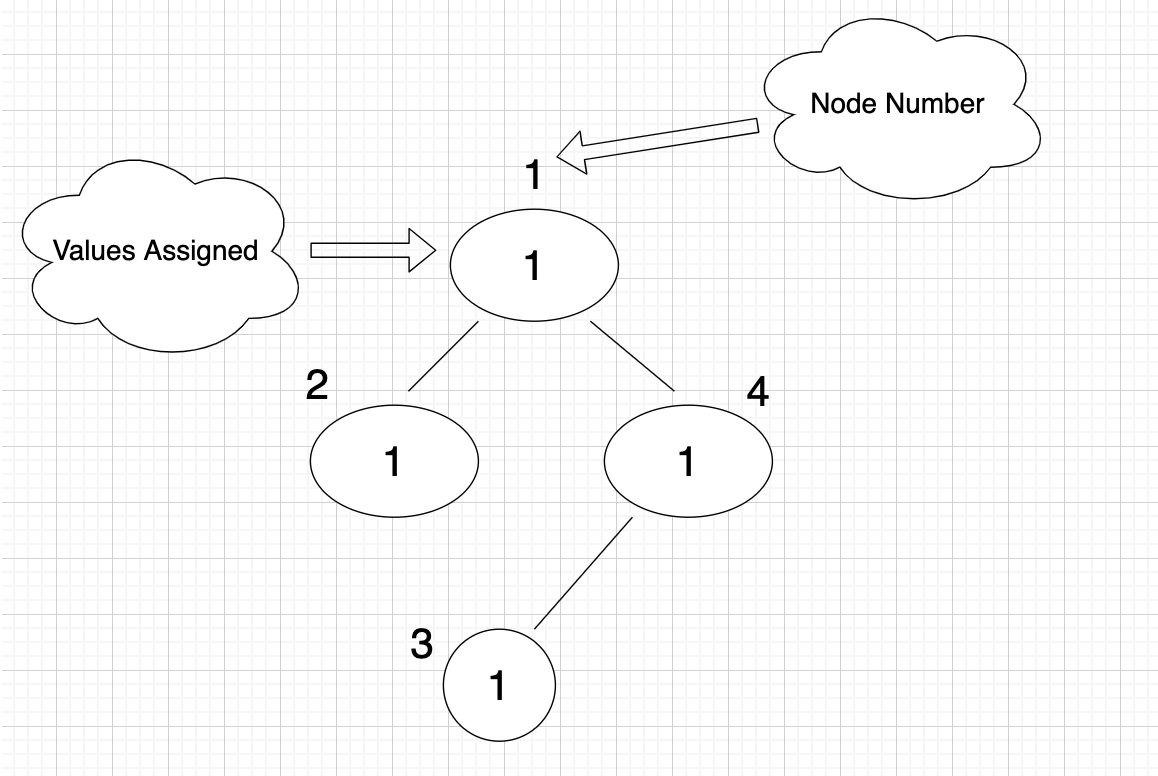
There are a total of 8 vertical paths:

1. 1
2. 2
3. 4
4. 2->1
5. 4->1
6. 3
7. 3->4
8. 3->4->1

But only (2 -> 1), (4 -> 1), (3 -> 4) have (cost of the path) % k = 0.

Hence the answer is 3.

Function Description

Complete the function countVerticalPaths in the editor below.

countVerticalPaths has the following parameters:

    cost: the array representing the value of each node.

    edge_nodes: number of nodes in the tree.

    edge_from: integer array where the i^th integer denotes one endpoint of the i^th edge.

    edge_to: integer array where the i^th integer denotes the other endpoint of the i^th edge

    k: an integer

Returns

    int: the number of vertical paths with (cost of the path) % k = 0

    Note: The tests are generated in such a way that the returned value fits in int32

Constraints

• 1 ≤ n ≤ 2*10⁵
• 0 ≤ cost[i]  ≤ 10⁸
• 1 ≤ k ≤ 10⁵

Input Format For Custom Testing

The first line contains one integer, n denoting the size of the cost array.

The next n lines contain elements of the cost array.

The next line contains two integers, n and m (where m = n - 1), denoting the number of nodes and number of roads respectively.

Each line i of the m subsequent lines (where 0 ≤ i < m) contains two integers, u and v, denoting that nodes u and v are connected via an edge.

The next line contains an integer denoting k.Sample Case 0

Sample Input For Custom Testing

STDIN         FUNCTION
-----         --------
5         ->  n = Size of Cost array.
1 
2
2
1
2         ->  cost = {1,2,2,1,2}
5 4       ->  n = 5, m = 4
2 3
2 1
1 4
2 5       
2         ->  k = 2

Sample Output

6

Explanation

There are 6 vertical paths following the given condition:

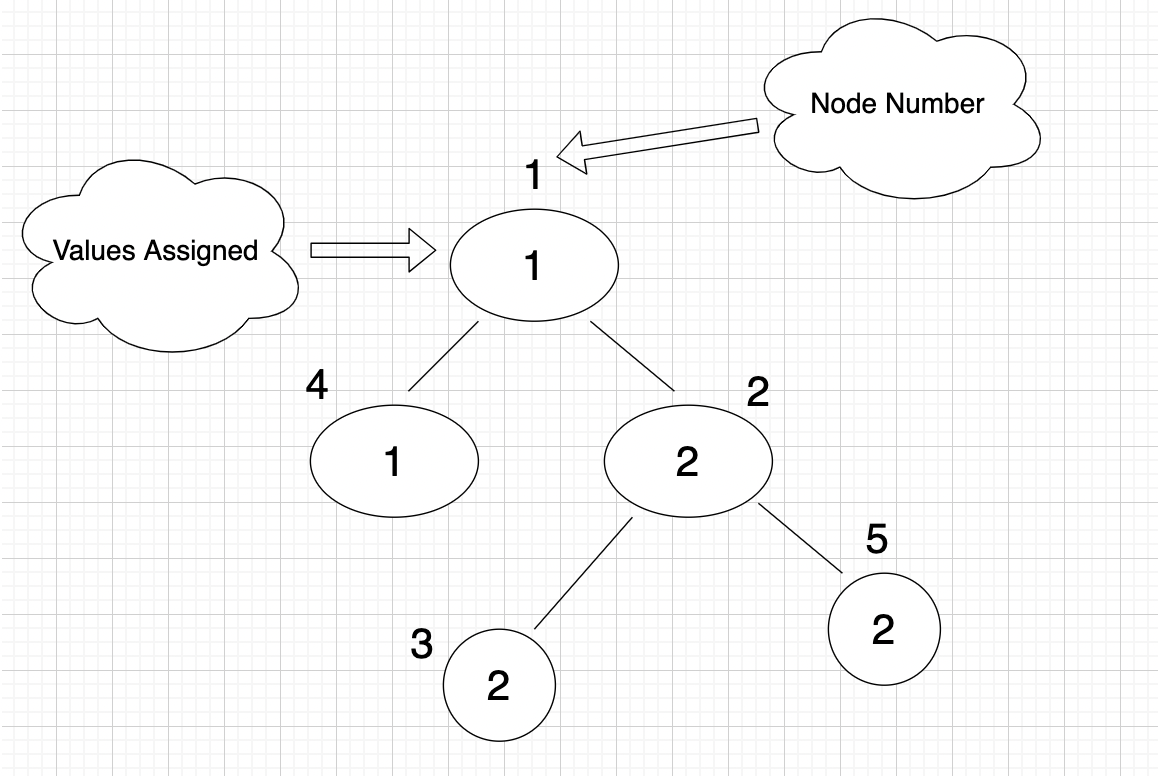
these paths are:

1. 2

2. 5 -> 2

3. 4 -> 1

4. 3

5. 3 -> 2

6. 5

Hence the answer is 6.Sample Case 1

Sample Input For Custom Testing

STDIN         FUNCTION 
-----         -------- 
5         ->  n = 5
2 
3
0
3
0         ->  cost = {2,3,0,3,0}
5 4       ->  n = 5, m = 4 
2 3         
3 1
3 4
3 5
3         ->  k = 3

Sample Output

7

Explanation

There are 7 vertical paths following the given condition :

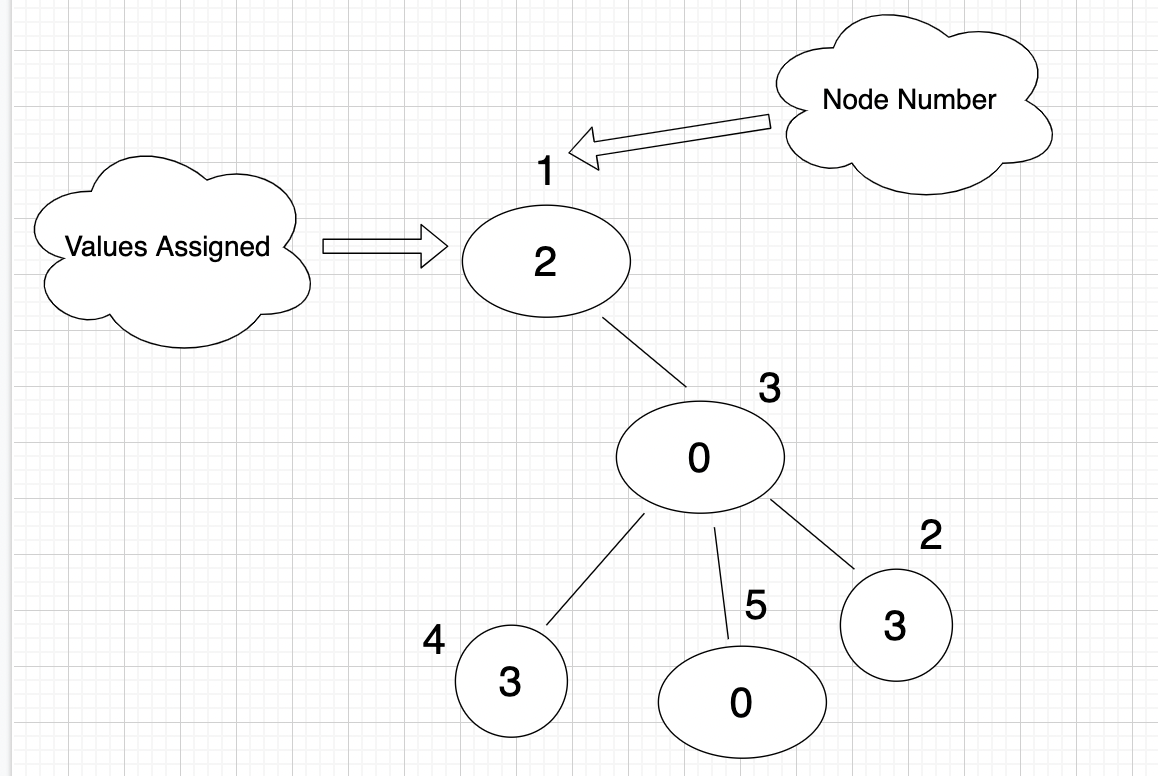
these paths are :

1. 4

2. 4 -> 3

3. 2

4. 2 -> 3

5. 5

6. 3

7. 5 -> 3

Hence the answer is 7.Language

#include·<bits/stdc++.h>

/*

·*·Complete·the·'countVerticalPaths'·function·below.

·*

·*·The·function·is·expected·to·return·an·INTEGER.

·*·The·function·accepts·following·parameters:

·*··1.·INTEGER_ARRAY·cost

·*··2.·UNWEIGHTED_INTEGER_GRAPH·edge

·*··3.·INTEGER·k

·*/

/*

·*·For·the·unweighted·graph,·<name>:

·*

·*·1.·The·number·of·nodes·is·<name>_nodes.

·*·2.·The·number·of·edges·is·<name>_edges.

·*·3.·An·edge·exists·between·<name>_from[i]·and·<name>_to[i].

·*

·*/

int·countVerticalPaths(vector<int>·cost,·int·edge_nodes,·vector<int>·edge_from,·vector<int>·edge_to,·

int·k)·{

}

int main()