Yet Another Tree Problem

 Nayra doesn't like stories of people receiving random trees as birthday presents, but this time she received a tree as a present for her own birthday! After struggling for a day trying to figure out what to do with this tree, she asked Aryan for help. He gave her this problem.

You are given a tree with N$N$ vertices and weighted edges. It is rooted at vertex 1$1$.

Define g(u,v)$g(u,v)$ to be the maximum weight of an edge on the shortest path between vertex u$u$ and vertex v$v$ in this tree.

Just calculating g(u,v)$g(u,v)$ is too easy, so you have to process Q$Q$ queries.

In each query, you are given K$K$ distinct vertices v1,v2,…,vK$v_1,v_2,\dots ,v_K$. You have to compute the sum of the g$g$-values of each pair of vertices among these K$K$, i.e, the value

∑i=1K−1∑j=i+1Kg(vi,vj)$$\sum _{i=1}^{K-1}\sum _{j=i+1}^{K}g(v_i,v_j)$$

Note: The input and output are large, so use fast input-output methods.

Input Format

• The first line of input contains a single integer T$T$ denoting the number of test cases. The description of T$T$ test cases follows.
• The first line of each test case contains two space-separated integers N$N$ and Q$Q$, denoting the number of vertices in the tree and the number of queries respectively.
• The second line contains N−1$N-1$ space-separated integers P2,P3,…,PN$P_2,P_3,\dots ,P_N$, where Pi$P_i$ is the parent of vertex i$i$.
• The third line contains N−1$N-1$ space-separated integers W2,W3,…,WN$W_2,W_3,\dots ,W_N$, where Wi$W_i$ is the weight of the edge between vertices i$i$ and Pi$P_i$.
• The next Q$Q$ lines contain queries you will have to answer. The description of Q$Q$ queries follows.
• The i$i$-th line contains an integer Ki$K_i$ followed by Ki$K_i$ distinct space-separated integers v1,v2,…,vKi$v_1,v_2,\dots ,v_{K_i}$, where Ki$K_i$ is the number of vertices in this query and v1,v2,…vKi$v_1,v_2,\dots v_{K_i}$ denote the vertices themselves.

Output Format

For each test, print one line containing Q$Q$ space-separated integers. The i$i$-th of these integers should be the answer to the i$i$-th query.

Constraints

• 1≤T≤3$1\le T\le 3$
• 10≤N≤105$10\le N\le {10}^5$
• 1≤Pi<i$1\le P_i<i$
• 1≤Wi≤5⋅106$1\le W_i\le 5\cdot {10}^6$
• 1≤Q≤3⋅104$1\le Q\le 3\cdot {10}^4$
• 10≤Ki≤N$10\le K_i\le N$
• 1≤vi≤N$1\le v_i\le N$
• All vi$v_i$ present in a single query are distinct
• It is guaranteed that the sum of Ki$K_i$ over all queries over all test cases in a single test file does not exceed 1.5⋅106$1.5\cdot {10}^6$
• It is guaranteed that the sum of Q$Q$ over all test cases in a single test file does not exceed 3⋅104$3\cdot {10}^4$

Sample Input 1 

1
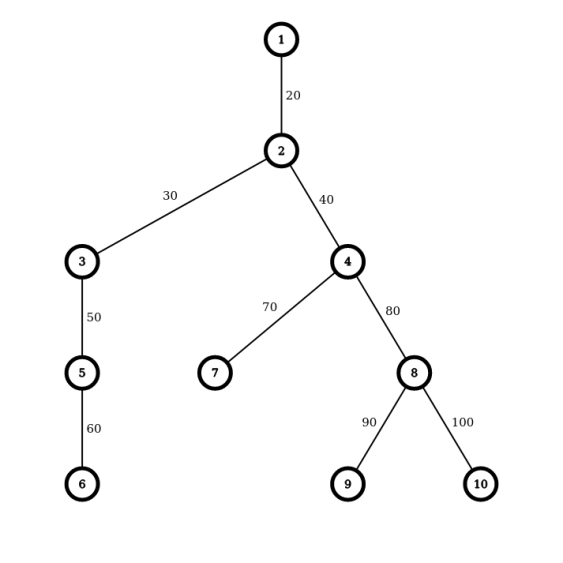
10 1
1 2 2 3 5 4 4 8 8
20 30 40 50 60 70 80 90 100
10 1 4 5 6 2 3 7 8 9 10

Sample Output 1 

3300

Sample Input 2 

1
10 2
1 2 2 3 5 4 4 8 8
20 30 40 50 60 70 80 90 100
4 1 4 5 6
4 2 3 7 8

Sample Output 2 

320 410

Explanation

In the second sample:

Let's look at different values of g(u,v)$g(u,v)$ for this tree.

For the first query, g(1,4)=40$g(1,4)=40$, g(1,5)=50$g(1,5)=50$, g(1,6)=60$g(1,6)=60$, g(4,5)=50$g(4,5)=50$, g(4,6)=60$g(4,6)=60$, g(5,6)=60$g(5,6)=60$. The sum of all these values is 320$320$.

For the second query, g(2,3)=30$g(2,3)=30$, g(2,7)=70$g(2,7)=70$, g(2,8)=80$g(2,8)=80$, g(3,7)=70$g(3,7)=70$, g(3,8)=80$g(3,8)=80$, g(7,8)=80$g(7,8)=80$. The sum of all these values is 410$410$.

Note: The second sample does not satisfy the constraint Ki≥10$K_i\ge 10$, so it won't be present in the actual test data. It's added here only for illustration.

Problem Code: YATP